Dr. Yong Xu

Dr. Yong Xu

Postdoc Working on Cosmology and Astroparticle Physics

你好, Hello!

My name is XU (徐) Yong (勇). I grew up in Xinyang, Henan, China. 🗣️ My mother tongue is the Xinyang dialect. I navigate between Mandarin and English, and possess a surviving-level proficiency in German. I earned my PhD 🎓 from the Universität Bonn in October 2022 and currently postdoc at Johannes Gutenberg-Universität Mainz.

My research focuses on the intersection of particle physics and cosmology. Motivated by curiosity and experimental advancements, I am particularly interested in investigating the physics from inflation to Big Bang Nucleosynthesis (BBN), concentrating on both theoretical developments and experimental implications. Here is my Inspire Page.

🌟 News 🌟: I will be joining McGill University this fall with a Trottier Space Institute Fellowship!

Recent Research Interests

  • Gravitational Wave from Graviton Production in the Early Universe
  • Multimessenger Probe of Physics before BBN
  • Probing the Nature of Dark Matter with Gravitational Waves
  • Black Hole as Laboratories to New Physics: Hawking Radiation, Superradiance, and Gravitational Atoms
  • Inflation and Its aftermath: Physics of (p)reheating, DM production and Mechanism of Baryogenesis
  • Modular Symmetry and Its application
  • Axion Cosmology
  • Cosmological perturbations, Primordial Black Hole formation and Induced Gravitational Wave Signatures

🌟 Research Highlight 🌟

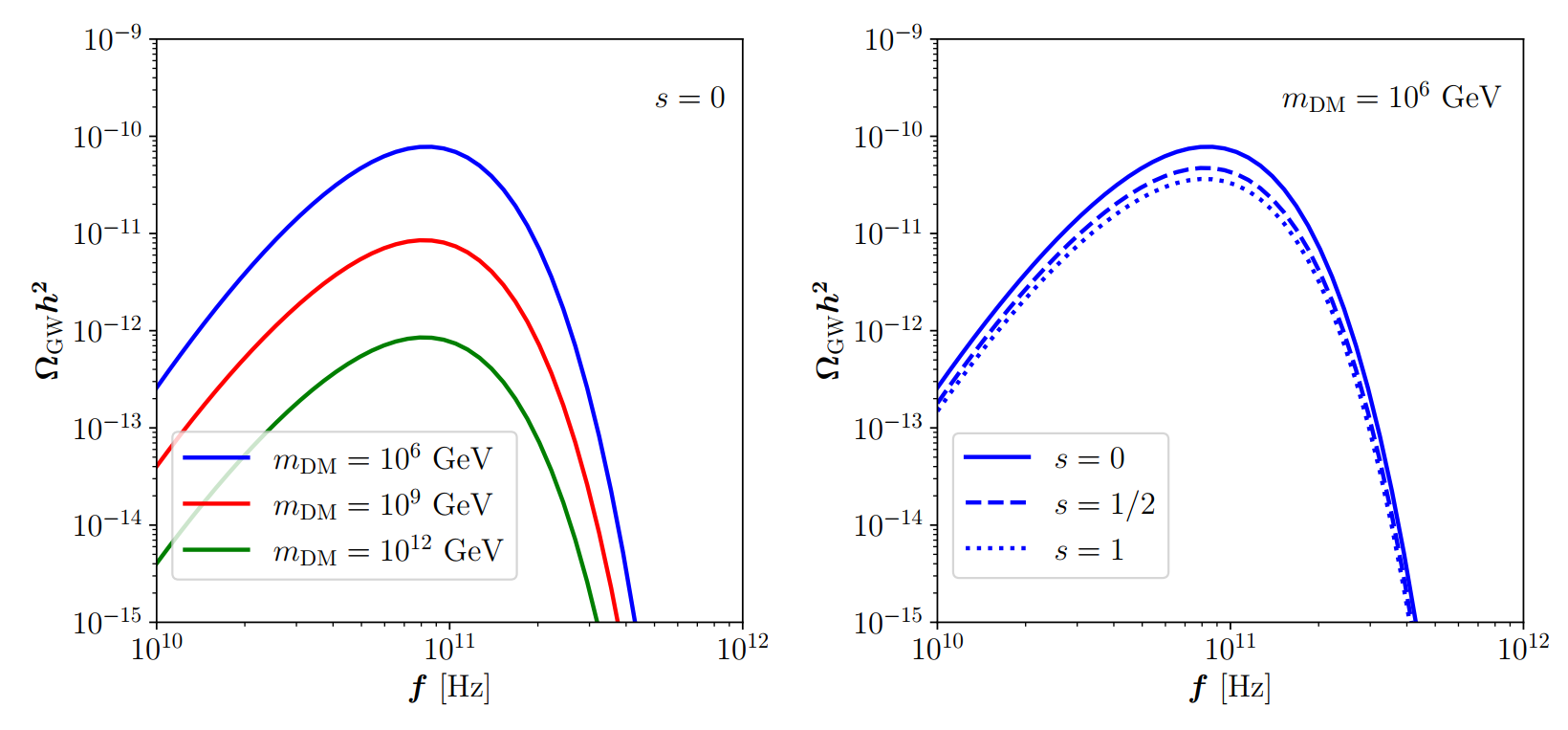
Probing Gravitational Dark Matter with Gravitational Waves

  • Pure Gravitational Dark Matter (PGDM) is the most minimal DM scenario, but would be very challenging for detection.

  • PGDM can be unavoidably generated in the early Universe via annihilation of particles in the SM plasma, where the latter also emits GWs.

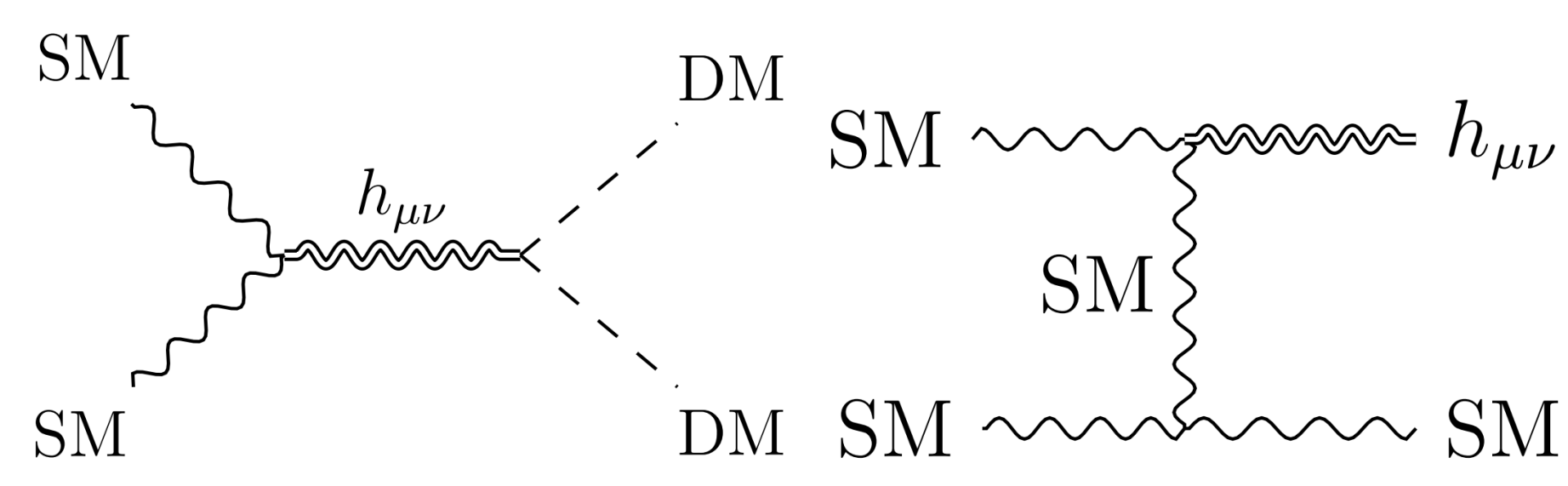
    Editing a markdown file for a talk

  • Such unavoidable cogenesis and tight connection imply that the GWs can help to probe the spin \(s\) and mass \(m_{\text{DM}}\) of PGDM.
  • For more information, see 2412.21137 and Phys.Lett.B 865 (2025) 139483

Editing a markdown file for a talk

Ultra-high Frequency Gravitational Waves from Scattering, Bremsstrahlung and Decay during Reheating

  • In 2407.03256, I systematically investigated the ultra-high frequency GWs from gravitons generated during inflationary reheating. The processes under consideration include: \((i)\) \(1 \to 3\) graviton Bremsstrahlung, \((ii)\) \(2 \to 2\) scattering of the inflaton and its decay products, \((iii)\) pure inflaton \(2 \to 2\) scattering, and \((iv)\) one-loop induced inflaton decay.
  • After a comprehensive comparison among the four sources of GWs, I identified the conditions under which dominant sources emerge.
  • A meaningful step toward establishing a more precise framework for identifying and analyzing the key sources of high frequency GWs in the early universe.

Editing a markdown file for a talk

Editing a markdown file for a talk

Probing Reheating With Axion Experiments

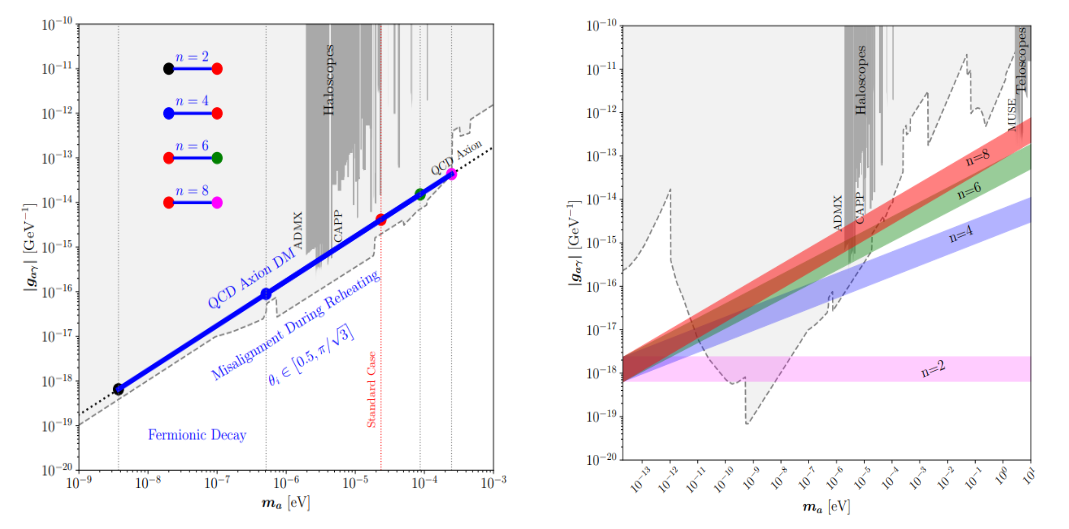
Editing a markdown file for a talk

Editing a markdown file for a talk

  • Axion/ALP production during reheating 2308.15322
  • Inflaton oscillating in a generic potential \(\phi^{n}\)
  • Extended axion parameter space depends on both the value of \(n\) and the type of inflaton matter coupling
  • Probing reheating via axion experiments!

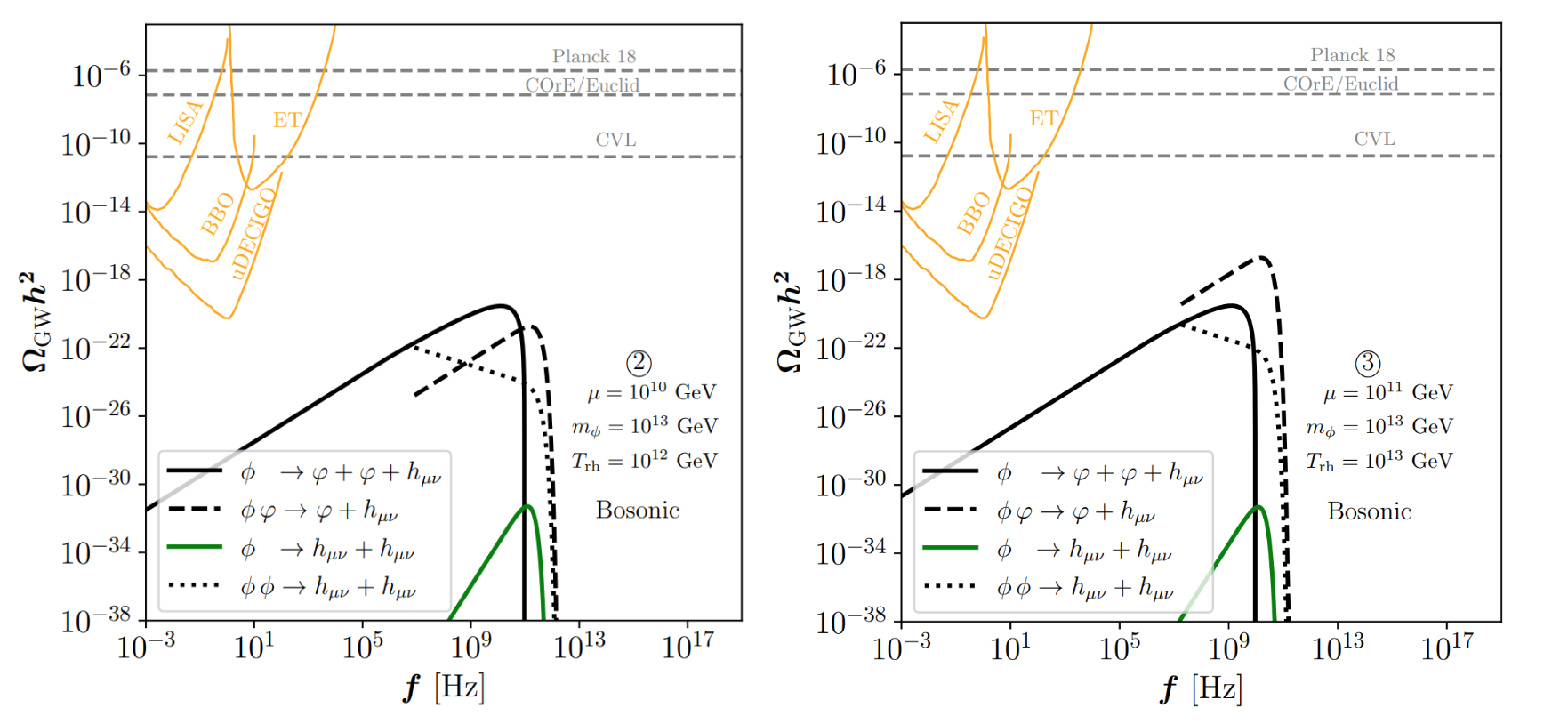
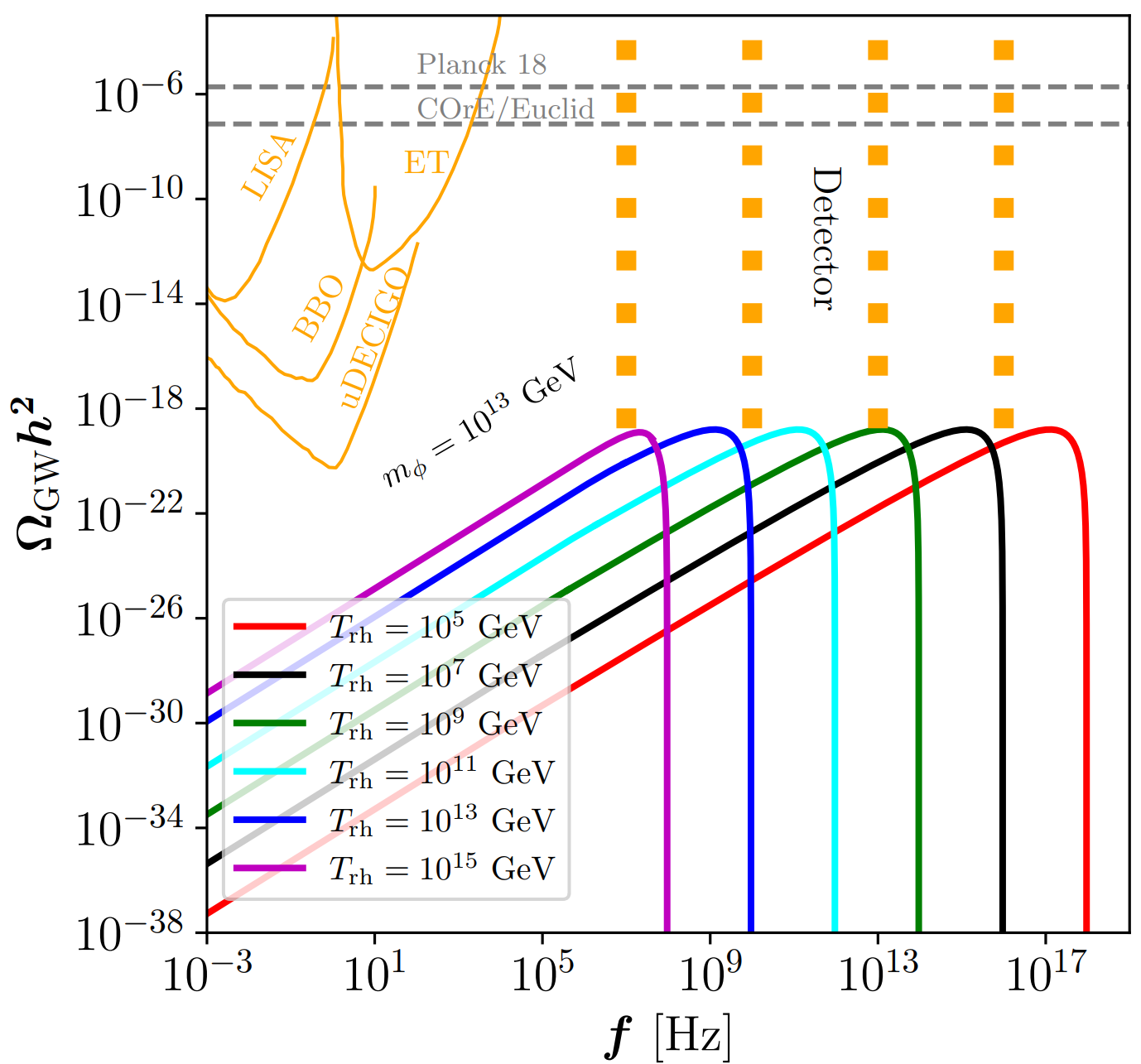
Probing Reheating with Bremsstrahlung GW

  • This is a proposal based on one of my recent paper 2407.03256 to use High-frequency Bremsstrahlung GWs to probe two important parameters: inflaton mass \(m_\phi\) and reheating temperature \(T_{\text{rh}}\)
  • Amplitude of peak \(\Omega_{GW}^{1\to3}h^2(f_{\text{peak}}) \simeq \mathcal{O} (10^{-18}) \left( \frac{m_\phi}{10^{13}~\text{GeV}}\right)^2\)
  • Location of peak frequency \(f_{\text{peak}}\simeq 9.5 \cdot10^{9}\,\left( \frac{m_\phi}{10^{13}~\text{GeV}}\right)\, \left(\frac{ 10^{13}~\text{GeV}}{T_{\text{rh}}}\right) \text{Hz}\)

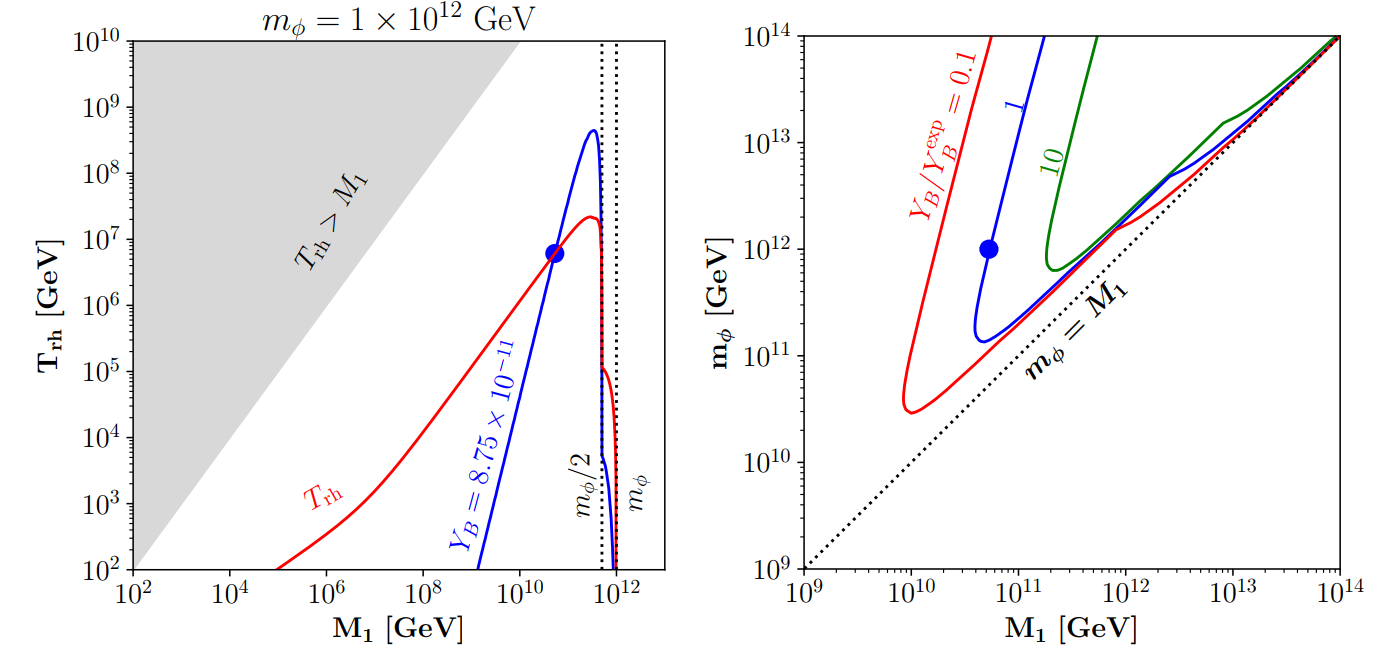
Editing a markdown file for a talk

Letogenesis from 3-body Decay

We recently found a novel channel for non-thermal leptogenesis via inflaton 3-body decay 2401.02485. The idea is very simple:

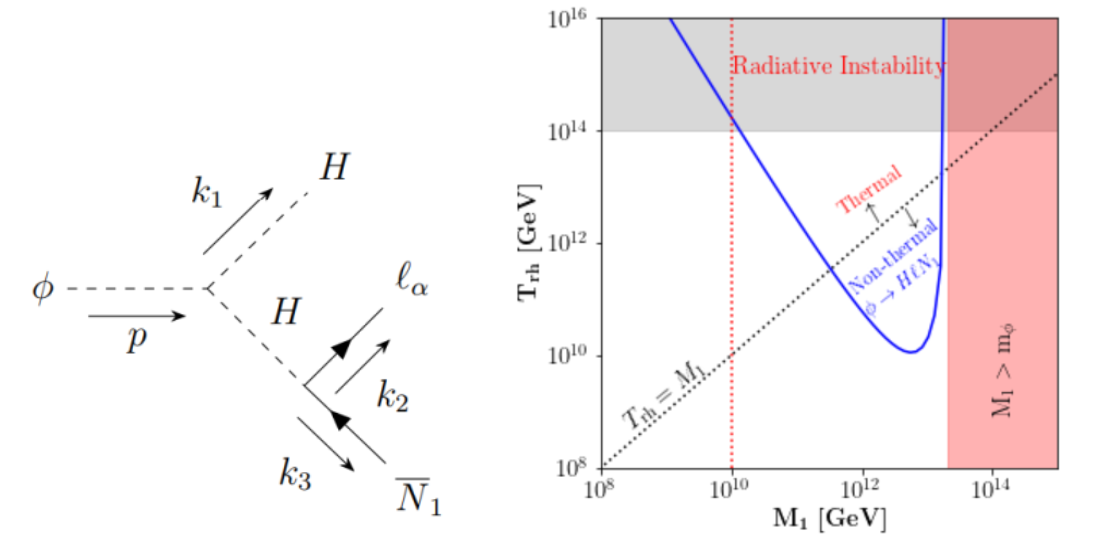
Editing a markdown file for a talk

  • One does not need to introduce (the traditional) \(\phi N N\) coupling
  • The only assumptions:
    • \(\phi H^{\dagger} H\) for reheating
    • \(H \ell N\) for neutrio mass via Type-I see-saw

Modular Symmetry and Cosmology

  • Modular symmetry offers nice explanations for the flavor puzzle, neutrino masses and mixings in the standard model, where the Yukawa couplings are treated as modular forms. Modular forms, which are holomorphic functions of the complex modulus \(\tau\), of a specific level (e.g., \(\Gamma_3\)) have a fixed structure that can reproduce observed lepton mass and mixing patterns.
  • The modular field \(\tau\) could drive the exponential expansion in the early Universe. After inflation, energy can be transferred from \(\tau\) to the standard model during reheating process.
  • In a recent work 2411.18603, we offered the first attempt to simultaneously address the lepton flavor problem, inflation, post-inflationary reheating, and baryogenesis via leptogenesis utilizing the modular group \(A_4\).
  • In our setup:
    • Lepton masses and mixings can be explained at \(1~\sigma\) level.
    • Light neutrino masses are generated via the Type-I see-saw mechanism.
    • Inflation is driven by the angular component of the modular field, \(\tau\), evolving along the arc of the fundamental domain.
    • Reheating of Universe after inflation proceeds via \(\tau\) decays into right handed neutrinos, Higgs and leptons.
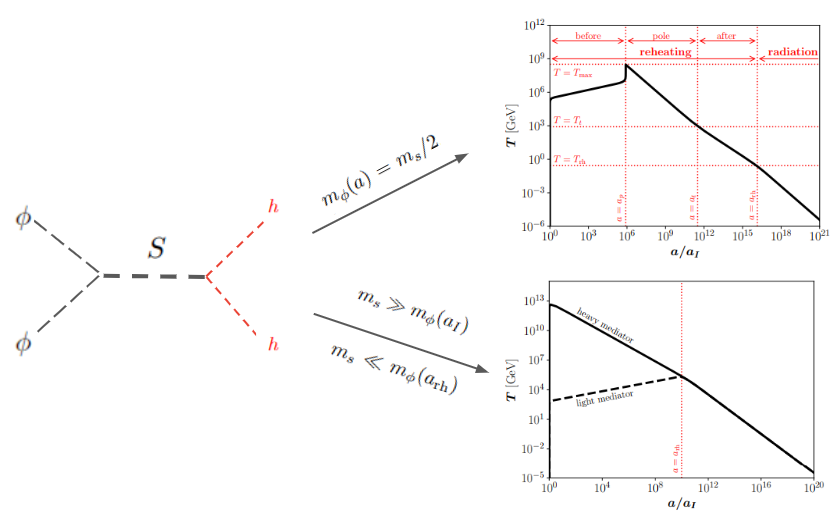
    • Baryon asymmetry of the universe (BAU) could be explained from Barygenesis via leptogenesis. Editing a markdown file for a talk

Resonant Reheating

  • Tradiational reheating via inflaton contact interaction such as \(\phi h^2\), \(\phi^2 h^2\)
  • For non-contact interactions, a massless graviton mediator has been discussed in lieterature
  • We explore reheating via inflaton annihilation via a massive mediator 2404.16090
  • Novel features show up, including
    • Resonant production of radiation and non-trival temperature evolution
    • Interesting implications on particle physics pheno and cosmo

Editing a markdown file for a talk

Dark Matter Production in the Early Universe

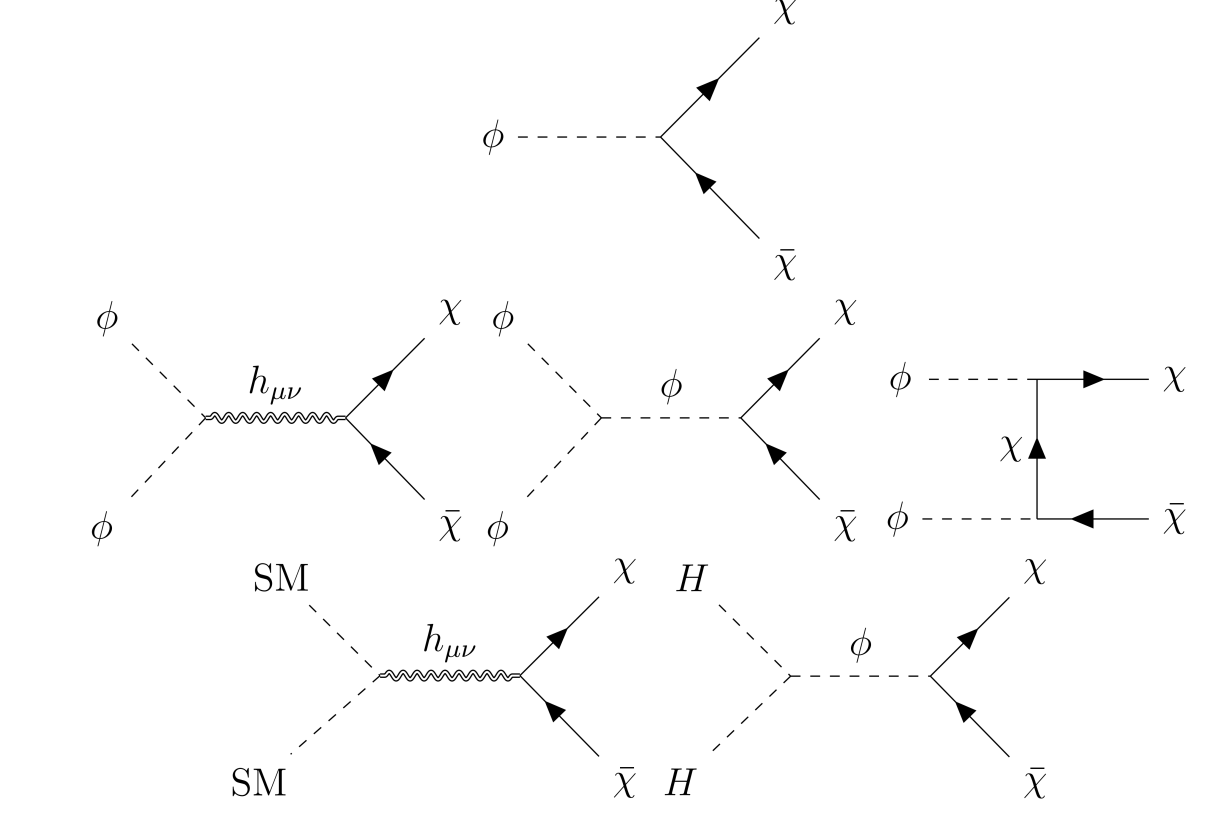
  • Dark Matter can be produced both non-thermally and thermally in the early Universe. Editing a markdown file for a talk
  • Considering all possible production channels can reveal interesting interplay between them, potentially altering the parameter space 2406.19447

Cosmic Inflation

  • Most simple chaotic inflation model \(V(\phi) \sim \phi^p\) with \(p>1/2\) has been ruled out by recent CMB experiments.
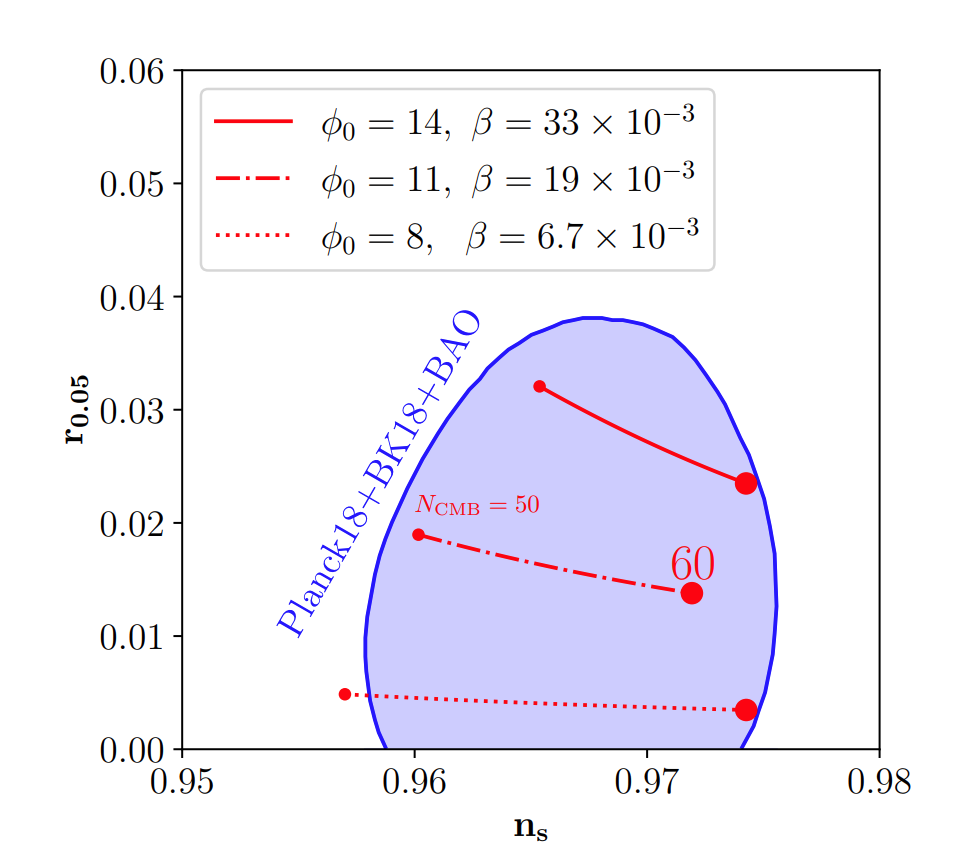
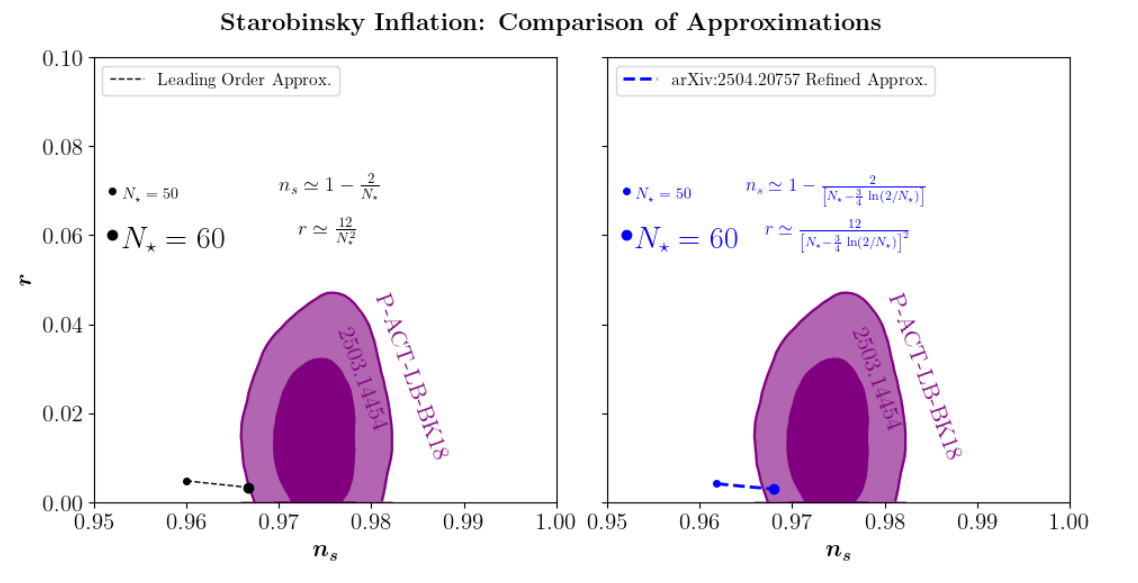
  • A simple and straightforward extension is a polynomial inflation model with a potential \(V(\phi) = a \phi^2 + b \phi^3 +d \phi^4\), which provides a good fit to the CMB data. It also predicts testable running of specal index and tensor-to-scalar ratio. See 2209.07545 for analysis in large field regime and 2104.03977 for analysis in small field scenario. Editing a markdown file for a talk

Refined Predictions for Starobinsky Inflation

  • The Starobinsky model, proposed in 1980, is a remarkably simple and predictive inflationary scenario.

  • We recently derived simple yet more accurate analytical approximations for the inflationary predictions, particularly for the spectral index \(n_s\), given by 2504.20757 \(n_s \simeq 1 - \frac{2}{N_\star - \frac{3}{4} \ln (2/N_\star)}\), \(r \simeq \frac{12}{\left[N_\star - \frac{3}{4} \ln (2/N_\star)\right]^2}\).

  • These refined approximations can reproduce the commonly used leading order expression in the literature, \(n_s \simeq 1 - \frac{2}{N_\star}\), \(r \simeq \frac{12}{N_\star^2}\), in the lagre \(N_\star\) limit. However, the commonly used approximations tend to underestimate the prediction for \(n_s\), potentially leading to misleading conclusions when comparing with precision observational data.

Editing a markdown file for a talk

Black Hole Superradiance, Dark Sector and GWs

A spinning black hole can effectively transmit energy to its surroundings through superradiance. When the Compton wavelength \(\lambda_C =1/m\) of a particle matches the gravitational radius \(r_g = G M_{\mathrm{BH}}\) of a black hole, the occupation number of the particles can undergo exponential amplification, resulting in the creation of “gravitational atoms” around the black hole. Superradiance condition: \(\frac{r_g}{\lambda_C}=G M_{\mathrm{BH}} \, m \simeq 0.38\left(\frac{M_{\mathrm{BH}}}{10^7 \mathrm{~g}}\right)\left(\frac{m}{10^7 \mathrm{GeV}}\right) \sim \mathcal{O}(1)\). This implies interesting phenomenology between:

  • Light BH and Heavy DM 2205.11522
  • (Super) Heavy BH and (Ultra) Light DM 🐣
  • Effects of superradiance “gravitational atoms” on waveforms of black hole binaries 🐣
  • GWs from “gravitational atoms” 🐣

Primordial Black Hole Formation

  • Is it possible to have PBH formation within the SM framework?
  • Yes. But we would need to fine-tune the top-quark mass to make the Higgs potential flat in the relevant region \(\sim 10^{17 -18}~\text{GeV}\).
  • If this occurs, it would lead to testable gravitational wave signatures that could be detected by DECIGO and BBO 1905.13581